数据结构完全指南：7种核心数据结构详解与Python实战代码

从入门到精通：快速掌握核心数据结构及其应用场景

Data Structure

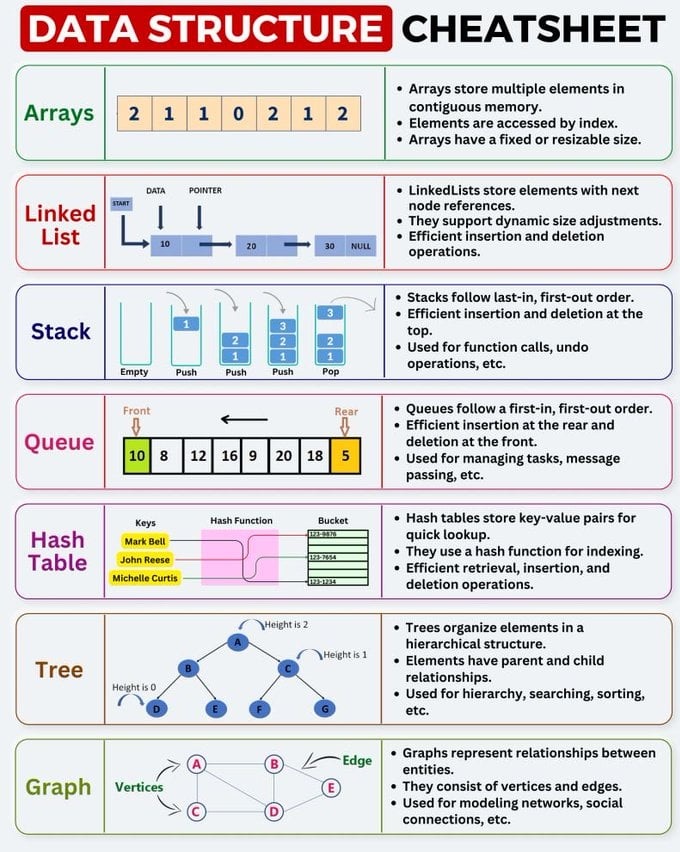
一、核心数据结构概览

让我们先从宏观上理解这七种基本的数据结构。

1. 数组 (Array)

• 核心概念：数组将相同类型的元素存储在连续的内存空间中。想象一个有编号的储物柜，每个柜子大小相同，紧挨着彼此。
• 关键特性：
  • 快速访问：通过索引（下标）可以直接定位到任何元素，时间复杂度为 $O(1)$。
  • 固定大小：在创建时通常需要指定大小，不易扩展。（动态数组，如 Vector 或 ArrayList，解决了这个问题，但扩容时有性能开销）。
  • 插入/删除慢：在数组中间插入或删除元素，需要移动后续所有元素，时间复杂度为 $O(n)$。
• 应用场景：需要频繁读取数据，而增删操作较少的场景。例如，存储一组固定的配置项、作为其他数据结构（如栈和队列）的底层实现。

2. 链表 (Linked List)

• 核心概念：链表中的元素（称为“节点”）在内存中是非连续存储的。每个节点除了包含数据外，还包含一个指向下一个节点的指针（引用）。
• 关键特性：
  • 动态大小：可以轻松地添加或删除节点，内存使用非常灵活。
  • 高效的插入/删除：只需要改变相邻节点的指针即可，时间复杂度为 $O(1)$（如果已知要操作的节点）。
  • 访问慢：查找一个元素必须从头节点开始，逐个遍历，时间复杂度为 $O(n)$。
• 应用场景：需要频繁进行插入和删除操作的场景。例如，实现任务队列、音乐播放器的播放列表、操作系统的内存管理等。

3. 栈 (Stack)

• 核心概念：栈是一种遵循后进先出 (LIFO - Last-In, First-Out) 原则的线性数据结构。想象一摞盘子，你总是先放上盘子，也总是从最上面取走盘子。
• 关键特性：
  • 只在栈顶进行插入（Push）和删除（Pop）操作。
  • 操作非常高效，均为 $O(1)$。
• 应用场景：
  • 函数调用栈：程序在调用函数时，会将函数信息压入栈，函数返回时再弹出。
  • 撤销/重做 (Undo/Redo) 操作。
  • 浏览器的历史记录（前进/后退）。
  • 括号匹配校验。

4. 队列 (Queue)

• 核心概念：队列是一种遵循先进先出 (FIFO - First-In, First-Out) 原则的线性数据结构。就像排队买票，先来的人先买到票。
• 关键特性：
  • 在队尾 (Rear) 进行插入（Enqueue），在队首 (Front) 进行删除（Dequeue）。
  • 操作非常高效，均为 $O(1)$。
• 应用场景：
  • 任务调度：管理待处理的任务，如打印机任务队列。
  • 消息传递：在不同系统模块间异步传递消息。
  • 广度优先搜索 (BFS) 算法。

5. 哈希表 (Hash Table)

• 核心概念：哈希表通过一个哈希函数 (Hash Function)，将“键 (Key)”映射到一个存储位置（“桶”或 “Bucket”），从而实现键值对 (Key-Value) 的快速访问。
• 关键特性：
  • 极快的查找、插入和删除：在理想情况下，时间复杂度接近 $O(1)$。
  • 可能会发生哈希冲突（不同的键映射到同一个位置），需要有解决冲突的机制（如链地址法、开放寻址法）。
• 应用场景：几乎无处不在！只要你需要快速通过一个唯一的标识符来存取信息，就应该首先考虑哈希表。
  • 数据库索引。
  • 缓存系统 (Caching)。
  • 编程语言中的字典 (Dictionary/Map) 实现。

6. 树 (Tree)

• 核心概念：树是一种分层的非线性数据结构，由节点和连接节点的边组成，具有清晰的父子关系。最顶端的节点是根节点，每个节点（除根外）只有一个父节点。
• 关键特性：
  • 层级关系：非常适合表示具有层级结构的数据。
  • 高效搜索：在特定类型的树（如二叉搜索树、B-树）中，搜索、插入、删除的效率很高，通常为 $O(\\log n)$。
• 应用场景：
  • 文件系统：目录和文件的组织结构。
  • HTML DOM：网页的结构就是一棵树。
  • 数据库索引（例如 B+ 树）。
  • 组织架构图。

7. 图 (Graph)

• 核心概念：图由顶点 (Vertices) 和连接顶点的边 (Edges) 组成，用来表示实体之间的复杂关系。与树不同，图中的节点之间可以有任意连接，甚至形成环。
• 关键特性：
  • 灵活性：可以模拟任何网络结构。
  • 边可以有方向（有向图）或权重（加权图）。
• 应用场景：
  • 社交网络：用户是顶点，好友关系是边。
  • 地图导航：地点是顶点，道路是边，距离是权重。
  • 计算机网络：设备是顶点，网络连接是边。
  • 推荐系统。

二、场景选择：我该用哪个？

面对一个具体问题时，如何选择最合适的数据结构？这里有一个简单的决策流程：

当你的需求是...	优先考虑	原因
快速通过索引访问元素，且数据量固定	数组	$O(1)$ 的读取速度无与伦比。
需要频繁地插入和删除元素，且不关心随机访问速度	链表	$O(1)$ 的增删操作效率极高。
需要管理一组“后进先出”的任务或数据	栈	完美契合 LIFO 场景，如函数调用、撤销操作。
需要按顺序处理任务，保证公平性	队列	FIFO 原则确保了处理的顺序性，如任务调度、消息队列。
需要通过唯一的键来快速存取、查找或删除值	哈希表	接近 $O(1)$ 的平均性能，是性能优化的首选。
需要表示层级关系、父子关系，或需要有序的数据集合	树	适合组织结构、文件系统等，二叉搜索树能提供 $O(\\log n)$ 的操作效率。
需要表示复杂的多对多关系、网络连接	图	社交网络、地图路径规划等问题的自然建模方式。

一个综合案例：

假设你要开发一个电商网站的购物车功能。

• 购物车里的商品列表：用数组或链表都可以。如果商品数量不多且固定，数组更简单；如果用户会频繁添加、删除商品，链表更灵活。
• 想快速通过商品ID找到购物车中的商品信息：用哈希表（商品ID -> 商品对象），这样更新数量、价格时可以 $O(1)$ 定位。
• 商品分类（如：电子产品 -> 手机 -> iPhone）：这显然是层级结构，应该用树来表示。
• 为用户推荐“购买了该商品的人还买了...”：这可以构建一个图，商品是顶点，用户同时购买的行为是连接它们的边。

针对 Python 的数据结构代码实战

1. 数组 (Array) -> Python 的 list

在 Python 中，我们通常使用 list 类型作为动态数组。它会自动处理内存分配和扩容，非常方便。

核心概念：Python 的 list 是一个动态数组，意味着它可以根据需要增长或缩小。它的元素在内存中是连续存储的（这使得索引访问非常快）。

# 1. 创建和初始化
# 创建一个包含整数的列表
my_array = [2, 1, 1, 0, 2, 1, 2]
print(f"初始列表: {my_array}")

# 2. 访问元素 (O(1) - 非常快)
# 通过索引访问第三个元素（索引从0开始）
element = my_array[2]
print(f"索引为2的元素是: {element}")

# 3. 修改元素 (O(1))
my_array[3] = 99
print(f"修改后的列表: {my_array}")

# 4. 添加元素
# a) 在末尾添加 (append) - 平均 O(1)
my_array.append(5)
print(f"在末尾添加5后: {my_array}")

# b) 在指定位置插入 (insert) - O(n)
# 在索引为1的位置插入数字88
my_array.insert(1, 88)
print(f"在索引1插入88后: {my_array}") # 注意：88后面的所有元素都向后移动了

# 5. 删除元素
# a) 删除末尾元素 (pop) - O(1)
last_element = my_array.pop()
print(f"删除末尾元素 ({last_element}) 后: {my_array}")

# b) 删除指定位置的元素 (pop) - O(n)
removed_element = my_array.pop(1) # 删除索引为1的元素
print(f"删除索引1的元素 ({removed_element}) 后: {my_array}")

# 6. 获取列表长度 (O(1))
print(f"当前列表长度: {len(my_array)}")

关键点：

• 优点：通过索引 my_array[i] 读写非常快。
• 缺点：在列表的开头或中间 insert 或 pop 会很慢，因为需要移动大量元素。

---

2. 链表 (Linked List)

Python 没有内置的链表类型，但我们可以用 class 轻松创建它。

核心概念：由节点 (Node) 组成，每个节点包含数据和指向下一个节点的引用 (next)。

# 首先定义节点类
class Node:
    def __init__(self, data):
        self.data = data  # 节点存储的数据
        self.next = None  # 指向下一个节点的引用，默认为None

# 然后定义链表类
class LinkedList:
    def __init__(self):
        self.head = None  # 链表的头节点，默认为None

    # 在链表末尾添加新节点
    def append(self, data):
        new_node = Node(data)
        if not self.head:  # 如果链表是空的
            self.head = new_node
            return
        # 否则，遍历到链表末尾
        last_node = self.head
        while last_node.next:
            last_node = last_node.next
        last_node.next = new_node

    # 打印链表所有节点的数据
    def display(self):
        elements = []
        current_node = self.head
        while current_node:
            elements.append(current_node.data)
            current_node = current_node.next
        print(" -> ".join(map(str, elements)))

# 使用链表
my_linked_list = LinkedList()
my_linked_list.append(10)
my_linked_list.append(20)
my_linked_list.append(30)

print("链表内容:")
my_linked_list.display() # 输出: 10 -> 20 -> 30

关键点：

• 插入和删除操作（如果知道目标节点的前一个节点）非常快，只需修改 next 引用，时间复杂度为 $O(1)$。
• 查找一个节点需要从 head 开始遍历，时间复杂度为 $O(n)$。

---

3. 栈 (Stack) - LIFO

在 Python 中，可以直接用 list 来模拟栈，因为 append() 和 pop() 操作在列表末尾都是 $O(1)$ 的。

# 使用列表实现栈
my_stack = []

# 入栈 (Push)
my_stack.append(1)
my_stack.append(2)
my_stack.append(3)
print(f"入栈后: {my_stack}") # 输出: [1, 2, 3]

# 出栈 (Pop)
top_element = my_stack.pop()
print(f"弹出的栈顶元素: {top_element}") # 输出: 3
print(f"出栈后: {my_stack}") # 输出: [1, 2]

# 查看栈顶元素 (Peek)
peek_element = my_stack[-1]
print(f"当前栈顶元素: {peek_element}") # 输出: 2

更优选择：使用 collections.deque。虽然 list 够用，但 deque (双端队列) 在两端添加和删除元素都经过了优化，是实现栈和队列的理想选择。

---

4. 队列 (Queue) - FIFO

用 list 实现队列是低效的，因为从列表头部删除元素 (pop(0)) 是 $O(n)$ 操作。正确的姿势是使用 collections.deque。

核心概念：deque 提供了 popleft() 方法，可以实现 $O(1)$ 复杂度的队首元素删除。

from collections import deque

# 使用 deque 创建队列
my_queue = deque()

# 入队 (Enqueue)
my_queue.append(10)
my_queue.append(8)
my_queue.append(12)
print(f"入队后: {my_queue}") # 输出: deque([10, 8, 12])

# 出队 (Dequeue)
front_element = my_queue.popleft() # O(1) 操作，非常高效！
print(f"出队的队首元素: {front_element}") # 输出: 10
print(f"出队后: {my_queue}") # 输出: deque([8, 12])

# 查看队首元素
if my_queue:
    print(f"当前队首元素: {my_queue[0]}") # 输出: 8

关键点：在需要实现队列时，请始终首选 collections.deque。

---

5. 哈希表 (Hash Table) -> Python 的 dict

Python 的字典 (dict) 就是一个功能强大且高度优化的哈希表实现。

核心概念：存储键值对 (key: value)，并通过哈希函数快速定位 key 对应的 value。

# 1. 创建和初始化
my_hash_table = {
    "Mark Bell": "123-4567",
    "John Reese": "321-7654",
    "Michelle Curtis": "456-1234"
}
print(f"哈希表: {my_hash_table}")

# 2. 访问元素 (平均 O(1))
# 通过 key 获取 value
phone_number = my_hash_table["John Reese"]
print(f"John Reese 的电话是: {phone_number}")

# 3. 添加或修改元素 (平均 O(1))
# 添加新条目
my_hash_table["Harold Finch"] = "999-9999"
# 修改现有条目
my_hash_table["Mark Bell"] = "111-2222"
print(f"修改后: {my_hash_table}")

# 4. 删除元素 (平均 O(1))
del my_hash_table["Michelle Curtis"]
print(f"删除后: {my_hash_table}")

# 5. 检查 key 是否存在 (平均 O(1))
if "Harold Finch" in my_hash_table:
    print("Harold Finch 在哈希表中。")

关键点：dict 是 Python 中最重要的数据结构之一。当你需要建立映射关系、快速查找时，它几乎总是最佳选择。

---

6. 树 (Tree)

和链表一样，树也需要我们自己用 class 来定义。下面是一个简单的二叉树节点定义。

class TreeNode:
    def __init__(self, key):
        self.key = key      # 节点的值
        self.left = None    # 左子节点
        self.right = None   # 右子节点

# 手动构建一棵树 (对应图片中的例子)
#     A
#    / \
#   B   C
#  / \ / \
# D  E F  G

# 创建节点
root = TreeNode('A')
root.left = TreeNode('B')
root.right = TreeNode('C')
root.left.left = TreeNode('D')
root.left.right = TreeNode('E')
root.right.left = TreeNode('F')
root.right.right = TreeNode('G')

# 遍历树 (例如：中序遍历 - 左、根、右)
def inorder_traversal(node):
    if node:
        inorder_traversal(node.left)
        print(node.key, end=' ')
        inorder_traversal(node.right)

print("树的中序遍历结果:")
inorder_traversal(root) # 输出: D B E A F C G

关键点：树的强大在于它的递归结构，许多操作（如搜索、遍历）都可以用简洁的递归函数来完成。

---

7. 图 (Graph)

在 Python 中，表示图最常见的方式是邻接表 (Adjacency List)，通常用一个字典来实现，其中每个键是一个顶点，值是与该顶点相邻的顶点列表。

# 使用字典和列表实现邻接表
# 对应图片中的例子
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'D'],
    'D': ['B', 'C', 'E'],
    'E': ['B', 'D']
}

# 打印图的结构
for vertex, neighbors in graph.items():
    print(f"顶点 {vertex} 连接到: {neighbors}")

# 查找一个顶点的所有邻居 (O(1))
print(f"\n顶点B的邻居是: {graph['B']}")

# 简单的图遍历算法：广度优先搜索 (BFS)
def bfs(graph, start_node):
    visited = set()     # 记录已访问的节点
    queue = deque([start_node]) # 从起始节点开始
    visited.add(start_node)
    
    while queue:
        vertex = queue.popleft()
        print(vertex, end=' ')
        
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

print("\n从顶点A开始的BFS遍历:")
bfs(graph, 'A') # 可能的输出: A B C D E

关键点：邻接表表示法对于稀疏图（边的数量远小于顶点数量的平方）非常节省空间，并且能快速找到一个顶点的所有邻居。

---