15种常见LeetCode算法技巧详解 - 算法面试必备
15种常见LeetCode算法技巧详解
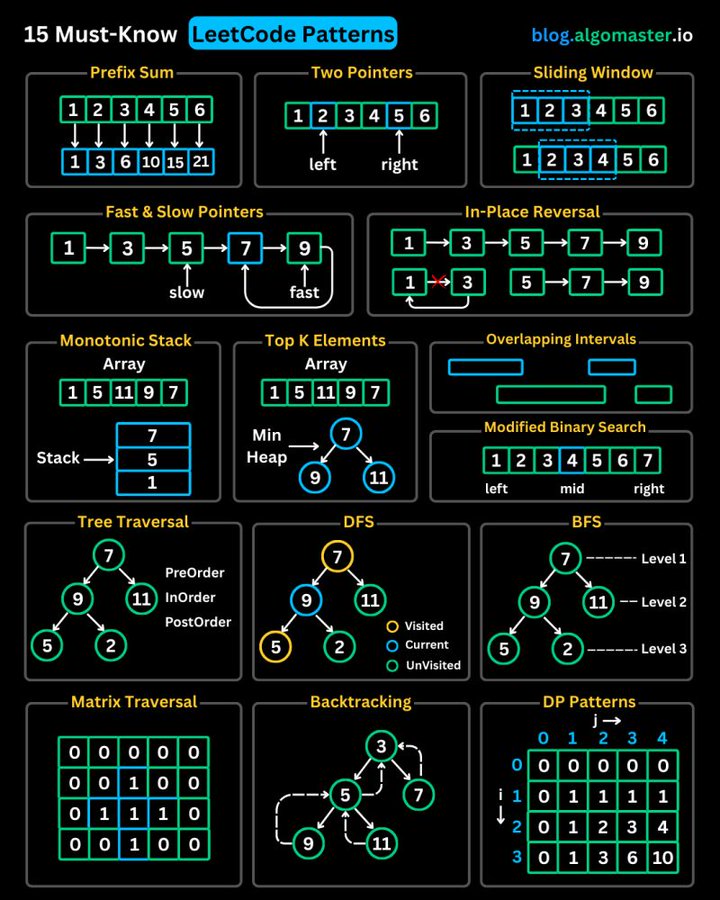
掌握这15种算法技巧,让你在LeetCode刷题和算法面试中游刃有余!本文详细解析每种技巧的核心思想、适用场景和实际例子。
目录
- 1. Prefix Sum(前缀和)
- 2. Two Pointers(双指针)
- 3. Sliding Window(滑动窗口)
- 4. Fast & Slow Pointers(快慢指针)
- 5. LinkedList In-place Reversal(链表原地反转)
- 6. Monotonic Stack(单调栈)
- 7. Top 'K' Elements(前K个元素)
- 8. Overlapping Intervals(区间重叠)
- 9. Modified Binary Search(变形二分查找)
- 10. Binary Tree Traversal(二叉树遍历)
- 11. Depth-First Search (DFS)
- 12. Breadth-First Search (BFS)
- 13. Matrix Traversal(矩阵遍历)
- 14. Backtracking(回溯)
- 15. Dynamic Programming(动态规划)
1. Prefix Sum(前缀和)
核心思想:提前计算数组前面一段的和,后面查询区间和就能很快得到。
📌 适合用在 区间求和 的场景。
例子:
数组 [2, 4, 5, 3, 1],想快速算出区间 [1, 3] 的和(4+5+3=12)。
- 普通方法:每次都累加,O(n)。
- 前缀和方法:先算出前缀和
[2, 6, 11, 14, 15],
再用prefix[3] - prefix[0] = 14-2 = 12。
👉 查询效率从 O(n) → O(1)。
2. Two Pointers(双指针)
核心思想:用两个指针在数组/链表上移动,减少不必要的重复遍历。
📌 常见于 有序数组、字符串比较。
例子:
判断数组 [1, 2, 4, 7, 11, 15] 中是否有两个数相加等于 15。
- 左指针在开头
1,右指针在结尾15。 - 如果和大了就右指针左移,小了就左指针右移。
👉 O(n) 就能完成。
3. Sliding Window(滑动窗口)
核心思想:用一个“窗口”来记录连续子区间,移动时只更新窗口内的值。
📌 用于 连续子串/子数组 问题。
例子:
找数组 [2, 1, 5, 2, 3, 2] 中长度为 3 的子数组最大和。
- 初始窗口
[2,1,5]→ 和=8 - 窗口右移,减去左边的数、加上右边的数 →
[1,5,2]→ 和=8 [5,2,3]→ 和=10 → 最大和=10。
👉 效率 O(n),比每次暴力求和 O(n*k) 快很多。
4. Fast & Slow Pointers(快慢指针)
核心思想:两个指针速度不同,用来检测循环或找到中点。
📌 常见于 链表、环检测。
例子:
判断链表是否有环。
- 快指针一次走两步,慢指针一次走一步。
- 如果有环,他们一定会相遇。
5. LinkedList In-place Reversal(链表原地反转)
核心思想:逐个翻转链表节点,改变指针指向。
📌 常见于 反转链表、K个一组反转。
例子:
链表 1 -> 2 -> 3 -> 4 → 反转后 4 -> 3 -> 2 -> 1。
做法:用三个指针(prev, curr, next)逐步翻转。
6. Monotonic Stack(单调栈)
核心思想:栈里保持单调(递增或递减),用来快速找到“下一个更大/更小元素”。
📌 常见于 下一个更大元素、直方图最大矩形。
例子:
数组 [2, 1, 2, 4, 3],求每个数右边第一个更大的数。
- 结果
[4, 2, 4, -1, -1]。
👉 用单调递减栈即可 O(n) 解决。
7. Top ‘K’ Elements(前 K 个元素)
核心思想:用最小堆/最大堆,快速找到前 K 大/小的元素。
📌 常见于 优先队列 问题。
例子:
找数组 [3, 1, 5, 12, 2, 11] 中最大的 3 个数。
👉 用最小堆维护 3 个数,最后得到 [5,11,12]。
8. Overlapping Intervals(区间重叠)
核心思想:先排序,再合并有重叠的区间。
📌 用于 日程安排、会议室问题。
例子:
输入区间 [(1,4), (2,5), (7,9)] → 合并后 [(1,5), (7,9)]。
9. Modified Binary Search(变形二分查找)
核心思想:二分查找不仅能找数,还能找边界、最接近的值等。
📌 常见于 旋转数组、最小值。
例子:
在旋转数组 [4,5,6,7,0,1,2] 中找最小值。
👉 用二分法不断缩小范围,最终找到 0。
10. Binary Tree Traversal(二叉树遍历)
核心思想:按不同顺序遍历树的所有节点。
📌 前序(根→左→右)、中序(左→根→右)、后序(左→右→根)、层序。
例子:
树:
1
/ \
2 3- 前序:1,2,3
- 中序:2,1,3
- 后序:2,3,1
- 层序:1,2,3
11. Depth-First Search (DFS)
核心思想:沿着一条路走到尽头,再回溯。
📌 常见于 树/图遍历、回溯。
例子:
迷宫问题:走到底之前不断递归,走不通就回头换路。
12. Breadth-First Search (BFS)
核心思想:一层一层往外扩散。
📌 常见于 最短路径、层序遍历。
例子:
求迷宫中从起点到终点的最短路径 → BFS 保证最早到达终点的一定是最短的。
13. Matrix Traversal(矩阵遍历)
核心思想:二维数组按行、列、方向遍历。
📌 常见于 岛屿问题、螺旋遍历。
例子:
统计二维网格里岛屿数量(1 表示陆地,0 表示水)。
👉 可以用 DFS/BFS 扫描相邻的 1。
14. Backtracking(回溯)
核心思想:尝试所有可能,当发现不合适就回退。
📌 常见于 全排列、组合、数独、八皇后。
例子:
全排列 [1,2,3] → 123, 132, 213, 231, 312, 321。
👉 回溯就是“做选择 → 递归 → 撤销选择”。
15. Dynamic Programming(动态规划)
核心思想:把大问题拆成小问题,保存结果避免重复计算。
📌 常见于 背包问题、最长子序列、路径规划。
例子:
斐波那契数列 F(n)=F(n-1)+F(n-2)。
- 递归会算很多重复值。
- DP 用数组存起来,效率 O(n)。
✅ 总结:
- 前缀和/双指针/滑动窗口 → 常用数组技巧
- 快慢指针/链表反转 → 针对链表
- 单调栈/Top K/区间合并/二分 → 高频面试技巧
- DFS/BFS/树遍历/矩阵遍历 → 图与树相关
- 回溯/动态规划 → 高级搜索与优化
from graphviz import Digraph
# 创建思维导图
dot = Digraph(comment="15种算法技巧思维导图", format="png")
dot.attr(rankdir="LR", size="10")
# 根节点
dot.node("root", "算法技巧", shape="ellipse", style="filled", fillcolor="lightblue")
# 一级分类
categories = {
"数组/序列技巧": ["Prefix Sum", "Two Pointers", "Sliding Window", "Fast & Slow Pointers"],
"链表技巧": ["LinkedList In-place Reversal"],
"栈与堆": ["Monotonic Stack", "Top 'K' Elements"],
"区间与二分": ["Overlapping Intervals", "Modified Binary Search"],
"树与图遍历": ["Binary Tree Traversal", "DFS", "BFS", "Matrix Traversal"],
"搜索与优化": ["Backtracking", "Dynamic Programming"]
}
# 添加分类节点和子节点
for cat, techniques in categories.items():
dot.node(cat, cat, shape="box", style="rounded,filled", fillcolor="lightyellow")
dot.edge("root", cat)
for tech in techniques:
dot.node(tech, tech, shape="note", style="filled", fillcolor="white")
dot.edge(cat, tech)
# 保存文件
output_path = "/mnt/data/algorithm_mindmap"
dot.render(output_path)
output_path + ".png"