Skip to main content

15 Essential LeetCode Algorithm Patterns - Complete Guide for Coding Interviews

Algorithm Learning Guide8/27/25...About 5 minAlgorithmsLeetCodeAlgorithmsInterviewCoding Patterns

15 Essential LeetCode Algorithm Patterns

LeetCode Algorithm Patterns
LeetCode Algorithm Patterns

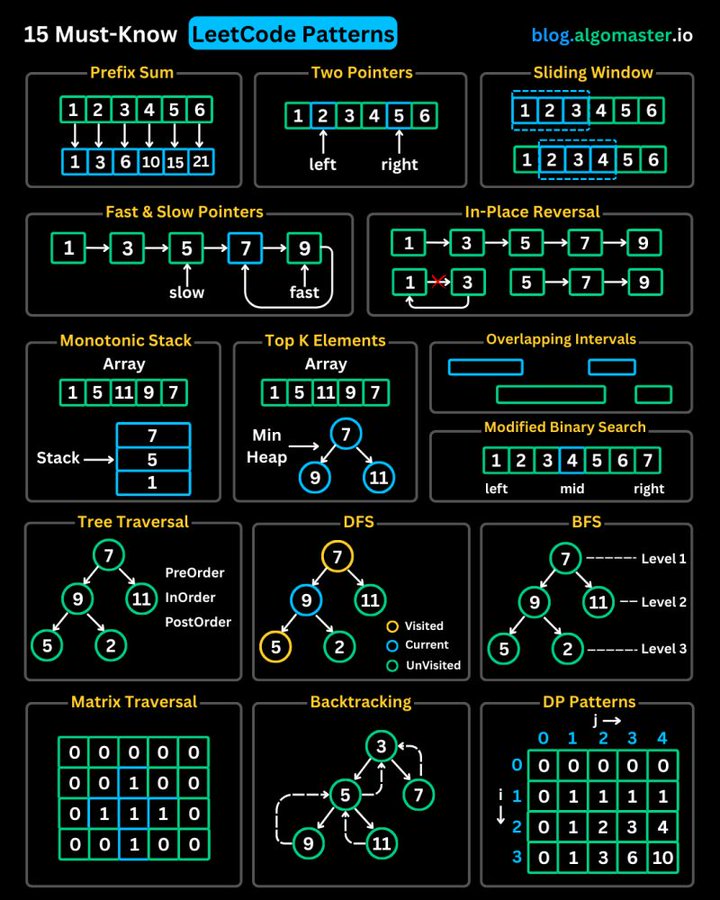
Master these 15 algorithm patterns to excel in LeetCode problems and coding interviews! This comprehensive guide explains the core concepts, use cases, and practical examples for each pattern.

Table of Contents

1. Prefix Sum

Core Concept: Pre-calculate cumulative sums of array elements to quickly compute range sums.
📌 Perfect for range sum queries.

Example:
Array [2, 4, 5, 3, 1], quickly calculate sum of range [1, 3] (4+5+3=12).

  • Naive approach: Sum elements each time, O(n).
  • Prefix sum approach: Pre-calculate prefix sums [2, 6, 11, 14, 15],
    then use prefix[3] - prefix[0] = 14-2 = 12.

👉 Query efficiency: O(n) → O(1).

2. Two Pointers

Core Concept: Use two pointers moving through array/linked list to reduce unnecessary iterations.
📌 Common in sorted arrays and string comparisons.

Example:
Check if array [1, 2, 4, 7, 11, 15] has two numbers that sum to 15.

  • Left pointer at start 1, right pointer at end 15.
  • If sum is too large, move right pointer left; if too small, move left pointer right.
    👉 Complete in O(n).

3. Sliding Window

Core Concept: Use a "window" to track continuous subarray, updating only window contents when moving.
📌 Used for continuous substring/subarray problems.

Example:
Find maximum sum of subarray of length 3 in [2, 1, 5, 2, 3, 2].

  • Initial window [2,1,5] → sum=8
  • Slide window right, subtract left element and add right element → [1,5,2] → sum=8
  • [5,2,3] → sum=10 → maximum sum=10.

👉 Efficiency O(n), much faster than brute force O(n*k).

4. Fast & Slow Pointers

Core Concept: Two pointers moving at different speeds to detect cycles or find middle points.
📌 Common in linked lists and cycle detection.

Example:
Detect if a linked list has a cycle.

  • Fast pointer moves two steps, slow pointer moves one step.
  • If there's a cycle, they will eventually meet.

5. LinkedList In-place Reversal

Core Concept: Reverse linked list nodes one by one by changing pointer directions.
📌 Common in reverse linked list and reverse K groups.

Example:
Linked list 1 -> 2 -> 3 -> 4 → reversed 4 -> 3 -> 2 -> 1.

Method: Use three pointers (prev, curr, next) to reverse step by step.

6. Monotonic Stack

Core Concept: Maintain monotonic order (increasing or decreasing) in stack to quickly find "next greater/smaller element".
📌 Common in next greater element and largest rectangle in histogram.

Example:
Array [2, 1, 2, 4, 3], find the first greater element to the right of each number.

  • Result [4, 2, 4, -1, -1].
    👉 Use monotonic decreasing stack to solve in O(n).

7. Top 'K' Elements

Core Concept: Use min/max heap to quickly find top K largest/smallest elements.
📌 Common in priority queue problems.

Example:
Find the 3 largest numbers in array [3, 1, 5, 12, 2, 11].
👉 Use min heap to maintain 3 numbers, result [5,11,12].

8. Overlapping Intervals

Core Concept: Sort first, then merge overlapping intervals.
📌 Used for scheduling and meeting room problems.

Example:
Input intervals [(1,4), (2,5), (7,9)] → merged [(1,5), (7,9)].

9. Modified Binary Search

Core Concept: Binary search can find not just values, but also boundaries and closest values.
📌 Common in rotated arrays and finding minimum values.

Example:
Find minimum value in rotated array [4,5,6,7,0,1,2].
👉 Use binary search to continuously narrow the range, finally find 0.

10. Binary Tree Traversal

Core Concept: Traverse all nodes in a tree in different orders.
📌 Preorder (root→left→right), Inorder (left→root→right), Postorder (left→right→root), Level order.

Example:
Tree:

    1
   / \
  2   3
  • Preorder: 1,2,3
  • Inorder: 2,1,3
  • Postorder: 2,3,1
  • Level order: 1,2,3

11. Depth-First Search (DFS)

Core Concept: Go as deep as possible along one path, then backtrack.
📌 Common in tree/graph traversal and backtracking.

Example:
Maze problem: Keep recursing until reaching the end, backtrack and try different paths when stuck.

12. Breadth-First Search (BFS)

Core Concept: Expand layer by layer outward.
📌 Common in shortest path and level-order traversal.

Example:
Find shortest path from start to end in a maze → BFS guarantees the first path to reach the destination is the shortest.

13. Matrix Traversal

Core Concept: Traverse 2D arrays by rows, columns, or directions.
📌 Common in island problems and spiral traversal.

Example:
Count number of islands in 2D grid (1 represents land, 0 represents water).
👉 Use DFS/BFS to scan adjacent 1s.

14. Backtracking

Core Concept: Try all possibilities, backtrack when finding unsuitable solutions.
📌 Common in permutations, combinations, Sudoku, N-Queens.

Example:
All permutations of [1,2,3] → 123, 132, 213, 231, 312, 321.
👉 Backtracking is "make choice → recurse → undo choice".

15. Dynamic Programming

Core Concept: Break big problems into smaller ones, save results to avoid repeated calculations.
📌 Common in knapsack problems, longest subsequence, path planning.

Example:
Fibonacci sequence F(n)=F(n-1)+F(n-2).

  • Recursion calculates many duplicate values.
  • DP stores results in array, efficiency O(n).

Summary

✅ Key Takeaways:

  • Prefix Sum/Two Pointers/Sliding Window → Common array techniques
  • Fast & Slow Pointers/LinkedList Reversal → For linked lists
  • Monotonic Stack/Top K/Interval Merging/Binary Search → High-frequency interview techniques
  • DFS/BFS/Tree Traversal/Matrix Traversal → Graph and tree related
  • Backtracking/Dynamic Programming → Advanced search and optimization

Algorithm Pattern Categories

from graphviz import Digraph

# Create mind map
dot = Digraph(comment="15 Algorithm Patterns Mind Map", format="png")
dot.attr(rankdir="LR", size="10")

# Root node
dot.node("root", "Algorithm Patterns", shape="ellipse", style="filled", fillcolor="lightblue")

# Categories
categories = {
    "Array/Sequence": ["Prefix Sum", "Two Pointers", "Sliding Window", "Fast & Slow Pointers"],
    "Linked List": ["LinkedList In-place Reversal"],
    "Stack & Heap": ["Monotonic Stack", "Top 'K' Elements"],
    "Intervals & Binary Search": ["Overlapping Intervals", "Modified Binary Search"],
    "Tree & Graph Traversal": ["Binary Tree Traversal", "DFS", "BFS", "Matrix Traversal"],
    "Search & Optimization": ["Backtracking", "Dynamic Programming"]
}

# Add category nodes and sub-nodes
for cat, techniques in categories.items():
    dot.node(cat, cat, shape="box", style="rounded,filled", fillcolor="lightyellow")
    dot.edge("root", cat)
    for tech in techniques:
        dot.node(tech, tech, shape="note", style="filled", fillcolor="white")
        dot.edge(cat, tech)

# Save file
output_path = "/mnt/data/algorithm_mindmap"
dot.render(output_path)

output_path + ".png"

This comprehensive guide covers the most essential algorithm patterns for LeetCode and coding interviews. Practice these patterns regularly to improve your problem-solving skills and interview performance.